第７弾：決定木を見通す

紹介論文

シリーズ第７弾で紹介する研究は、柏山美結さんが修士２年のときに行った以下の研究です。

概要

　柏山さんが行った研究は「決定木が良くなっていく過程をわかりやすく可視化する」というものです。でも、これでは何をしたのかほとんど想像できないだろうと思います。そこで、まずは「決定木」が何なのかを説明し、次にそれが次第に良くなっていくというのがどういうことなのかを説明します。その上で、本題である可視化の話に移っていきましょう。

決定木

　ここに、とあるアイスクリーム屋さんで、一日あたりいくつのアイスクリームが売れたかを示す表があったとしましょう。次のようなものです。

表１ : アイスクリームが売れた数の例

日付	曜日	季節	天気	最高気温	売れた個数
2025/1/19	日曜	冬	曇り	6 度	158 個
2025/1/20	月曜	冬	晴れ	8 度	87 個
⋮
2025/3/14	金曜	春	雨	14 度	105 個
2025/3/15	土曜	春	曇り	11 度	174 個
⋮
2025/8/4	月曜	夏	晴れ	34 度	388 個
2025/8/5	火曜	夏	晴れ	32 度	323 個
⋮

　表１ には、日付とその日の天気などの情報、そしてその日にいくつのアイスクリームが売れたのかが順に書かれています。最近では、このようなデータが多くの店で蓄積されています。このデータから、いろいろな状況下でいくつのアイスクリームが売れそうかを予測したいとしましょう。例えば、夏の晴れた日なら 400 個くらい売れるかも知れませんが、冬の雨の日なら 100 個くらいだろうといったことです。

　このシリーズでは、これまで大量のデータから情報を得るために深層学習を用いる研究を紹介してきました。深層学習を使うと、大量に用意したデータを学習することで、どのような日だったらいくつくらい売れるかを次第に予測できるようになって いきます。しかし、深層学習も万能というわけではありません。深層学習の最大の欠点は、どうしてそのくらい売れそうと判断したのか、その根拠を教えてはくれないところです。売り上げを知りたい日の状況を入れると、いくつくらい売れそうかという数字は出してくれるのですが、なぜ、そのくらいの個数になるのかはわからないのです。

　このような理由で、実際の現場では深層学習以外の手法が使われることも多々あります。そのようなときに使われる手法のひとつが決定木です。決定木というのは、いくつかの質問に順番に答えていくと、アイスクリームがいくつくらい売れそうかを答えてくれるものです。ひとつ例を見てみましょう。

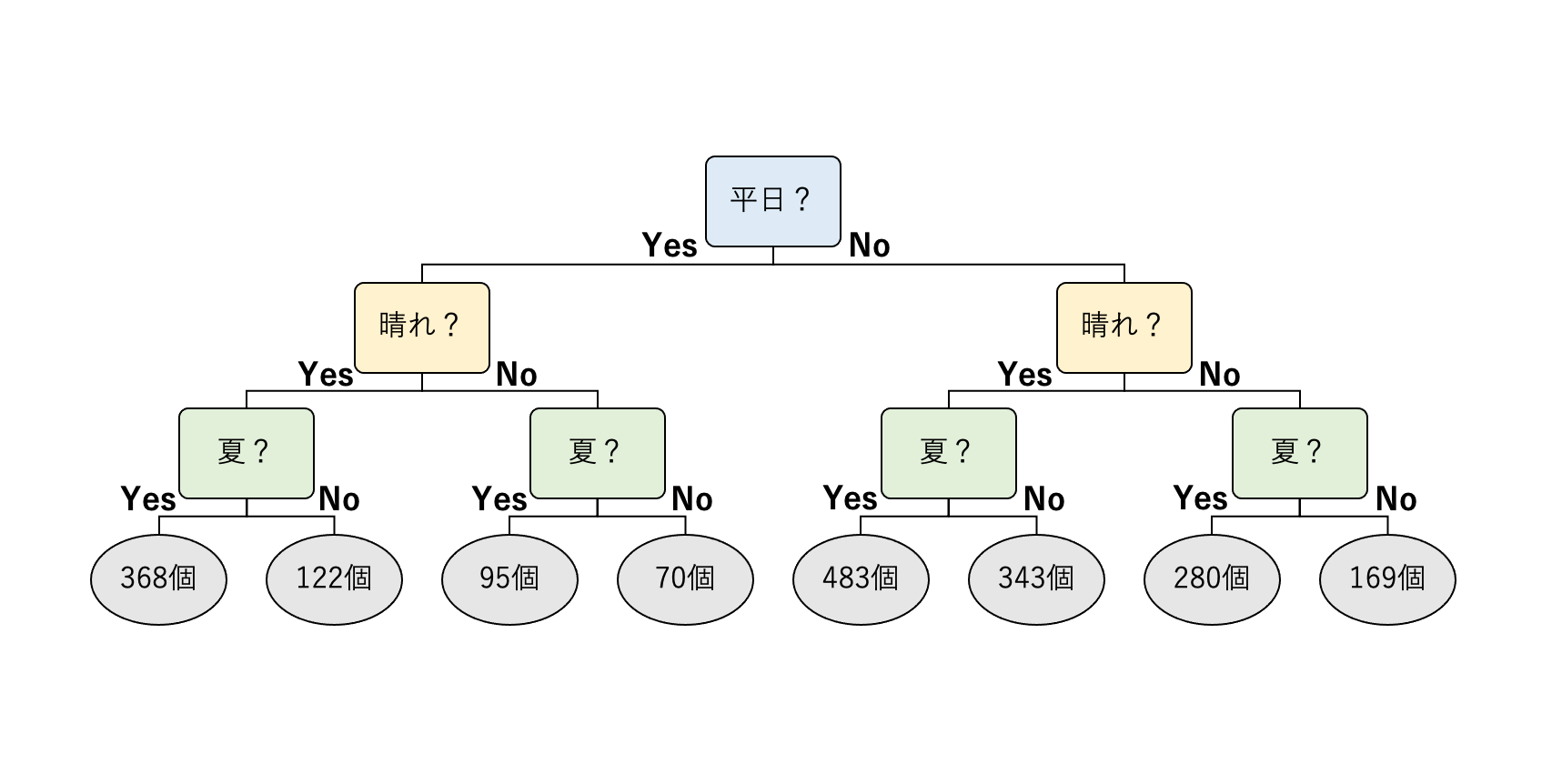
　図１に示す決定木は、いろいろな状況のもとで一日あたりいくつくらいのアイスクリームが売れるのか、その予測値を返します。決定木の各部分には質問が書かれていて、その質問に答えていくと、その条件のもとでの予測値がわかるようになっています。

　図１の決定木では、まず来店した日が平日かどうかで場合分けをしています。平日だったら左に、平日でなかったら右に移動します。次は、その日の天気が晴れだったかどうか、さらに、季節が夏かどうかで場合分けをしています。決定木の一番下までくると、その日にいくつアイスクリームが売れそうかの予測値がわかります。例えば、表１の最初の日なら、冬の休日の曇りの日なので169 個というのが決定木による予測値になります。表１では 158 個となっていますので、実際の値とはずれていますが、近い値になっています。

　このように、順番に質問に答えていくことで欲しい情報を提供するのが決定木です。決定木を使うとどのくらいの数のアイスクリームが売れるのかがわかるだけでなく、どのような場面のときにそれだけ売れるのかがわかります。個数だけなら深層学習を使ったアプローチを使っても得られますが、決定木を使うとその状況まで把握することができるのです。

決定木の誤差

　 　決定木を使うと簡単に予測値を得ることができます。でも、その予測値はどのくらい正確なのでしょうか。先ほど見た「冬の休日の曇りの日」の例では、予測値は 169 個でしたが実際には 158 個でした。ここには 11 個の差があります。このように、予測値と実際の値との間には誤差（ずれ）があります。そうすると、いろいろな入力に対して、この誤差がなるべく小さいものがより良い決定木と言えそうです。

　決定木は、いくつかの質問によって場合分けをしているだけなので、全ての場合に対して完璧に結果を予測できるとは思えません。でも、上手に決定木を作ったら、誤差の小さい決定木を作ることはできるのでしょうか。ここでは、そのような決定木を作る手法として勾配ブースティング決定木と呼ばれるものを紹介します。勾配ブースティング決定木の特徴は、たくさんの決定木を使って結果を出すこと、そのたくさんの決定木を単純な決定木から始めて次第に誤差を小さくするようにして作っていくことです。次の節では、勾配ブースティング決定木で使われるたくさんの決定木をどのように作るのか、そしてそこからどのようにして誤差の少ない予測値を返すのかを説明してきます。

勾配ブースティング決定木

　勾配ブースティング決定木では、たくさんの決定木を順になるべく誤差が小さくなるように作っていきます。

　ふたたびアイスクリーム屋さんの例を考えてみましょう。勾配ブースティング決定木で、最初に作る決定木は「どんな入力に対しても、いつも同じ個数を答える」ようなものです。普通、ここで答える個数は全データの平均値、つまり表１の「売れた個数」の列の平均値をとります。仮にここではその値を 208 個としておきましょう。どんな入力に対しても 208 個と答えるので、この決定木はほとんど役に立ちません。でも、具体的な状況が何もわからないなら、全体の平均値を返すというのは妥当そうに見えます。また、この決定木は質問がひとつもないとても簡単な形をしていることにも注目しましょう。質問の多い決定木はより詳細に状況を分析できますが、あまりに質問が多い決定木は細部にこだわり過ぎて大局の見えないもの、特定の場面に特化し過ぎた汎用性の少ないものになりがちです。勾配ブースティング決定木で作る決定木は、とても単純な決定木から始めることで、決定木が過度に複雑になりすぎるのを避けています。

　勾配ブースティング決定木では、このような「単に平均値を返す決定木」から始めて、誤差を小さくするように新たな決定木を追加していきます。まずこの決定木が返す値（つまり 208 個）と実際の値との誤差を出します。すると次の表のようになります。例えばこの表の最初の行では、売れた個数は 158 個ですが、平均は 208 個なので、その間の誤差は 158 - 208 = -50 個となります。

表２: 売れた個数と予測値1（平均）の間の誤差

日付	曜日	季節	天気	最高気温	売れた個数	予測値1	誤差1
2025/1/19	日曜	冬	曇り	6 度	158 個	208 個	-50 個
2025/1/20	月曜	冬	晴れ	8 度	87 個	208 個	-121 個
⋮
2025/3/14	金曜	春	雨	14 度	105 個	208 個	-103 個
2025/3/15	土曜	春	曇り	11 度	174 個	208 個	-34 個
⋮
2025/8/4	月曜	夏	晴れ	34 度	388 個	208 個	180 個
2025/8/5	火曜	夏	晴れ	32 度	323 個	208 個	115 個
⋮

　全てのデータについて誤差を計算できたら、次は「誤差を予測するような決定木」を作ります。どのようにして作るかには触れませんが、たくさん与えられた誤差データを上手に予測できるように学習を行います。その際、最も良さそうな決定木に向かって（勾配の最も急な道を選んで）進んでいくことから勾配ブースティング決定木という名前がついています。

　得られる決定木は、例えば、次の図のようなものになります。

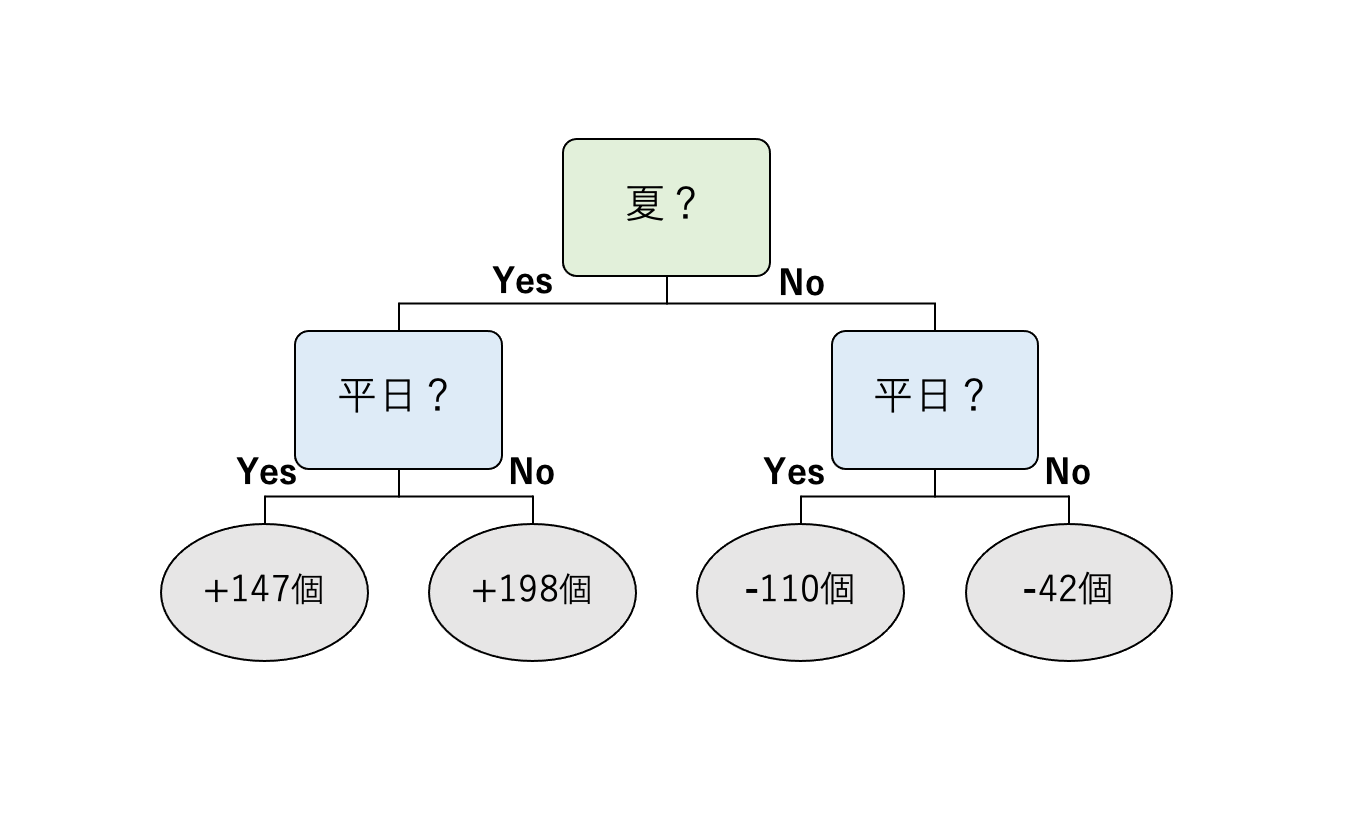
　図２の決定木は、図１の決定木と似た形をしていますが、最後に返す値が誤差であるところが異なります。例えば、夏の平日の場合は +147 個という値が返ってきますが、これは夏の平日は平均よりも 147 個くらい多くのアイスクリームが売れていることを示しています。逆に、冬の平日なら平均よりも 110 個ほど売り上げは減っていることを示しています。

　このような決定木を得られたら、この誤差の分だけ補正してあげれば予測値はよくなりそうです。つまり、ひとつ目の決定木の結果（＝平均値）に図２の決定木によって得られた誤差分を加えてあげれば実際の値に近づきます。ですが、勾配ブースティング決定木では誤差分をそのまま加えることはしません。差分を全部、加えるのではなく「少しだけ」加えます。この加える割合は学習率と呼ばれます。例えば、学習率が 0.5 であれば、誤差の半分を加えます。これを行った結果の表を以下に示します。

表３: 売れた個数と予測値2 の間の誤差

日付	曜日	季節	天気	最高気温	売れた個数	予測値1	誤差1	予測値2	誤差2
2025/1/19	日曜	冬	曇り	6 度	158 個	208 個	-50 個	183 個	-25 個
2025/1/20	月曜	冬	晴れ	8 度	87 個	208 個	-121 個	148 個	-61 個
⋮
2025/3/14	金曜	春	雨	14 度	105 個	208 個	-103 個	157 個	-52 個
2025/3/15	土曜	春	曇り	11 度	174 個	208 個	-34 個	191 個	-17 個
⋮
2025/8/4	月曜	夏	晴れ	34 度	388 個	208 個	180 個	298 個	90 個
2025/8/5	火曜	夏	晴れ	32 度	323 個	208 個	115 個	265 個	58 個
⋮

　予測値 2 は予測値 1 に誤差 1 の半分を加えた値になっています。例えば、最初の行では 208 + (-50) / 2 = 183 個となります。

　誤差分を加えてあげると、予測値が少し実際に売れた個数に近付いていることがわかります。誤差分を 100% 加えてあげればもっと実際に売れた個数に近づくのですが、それをせずに学習率分だけしか近づけないのは過学習を防ぐためです。図２の決定木は、夏かどうか、平日かどうかという観点から誤差を減らそうとしています。これは、たまたま表２の誤差を表現するには、このふたつの観点で場合分けをするのが良いと学習したためです。でも、この結果を重視しすぎると、この場合にしかうまく動かないものになってしまいます。これを過学習と呼びます。過学習を避けるため、学習率を用いて適切な分だけ組み込むようにしています。

　さて、表３になって少し誤差が縮まりましたが、まだ誤差は残っています。この誤差をさらに小さくして精度を高くするため、次の決定木を作ります。これは、ここまで見てきた方法を繰り返すだけです。つまり、表３の予測値 2 と実際に売れた個数との間の誤差を計算し、その誤差を予測するような決定木を作ります。例えば、次のような決定木が得られます。

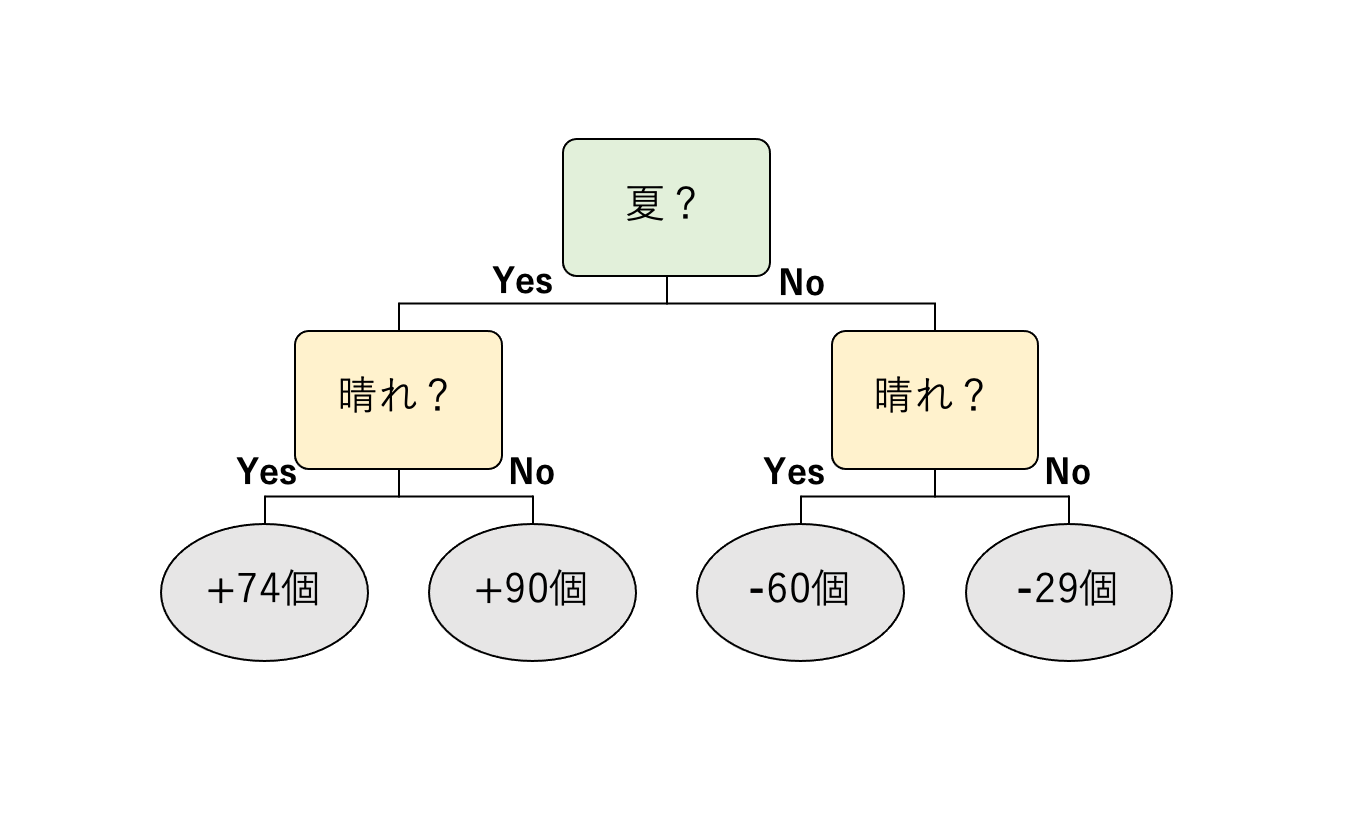
　新たな決定木が得られたら、こちらにも適当な学習率をかけて予測値に足しこむことで、さらに誤差の少ない予測値を求めていきます。このような過程を繰り返すことで、全体として精度の高い決定木を作っていくのが勾配ブースティング決定木です。

　図２と図３では、質問が変化していることに注意をしてください。最初の質問はどちらも「夏かどうか」ですが、ふたつ目の質問は異なっています。さらに、これまでは考慮していなかった最高気温についての質問が使われることもあります。このように、学習が進んでいくと別の質問も組み込まれ、これらを通してより正確な予測ができるようになっていきます。

決定木の可視化

　さて、ここまで決定木と、その進化版である勾配ブースティング決定木を見てきました。勾配ブースティング決定木では、複数の決定木を上手に学習していくことで精度の高い予測を実現しています。一方で、たくさんの決定木が出てきて、それらの結果が学習率の重みで足し合わされるなど、仕組みは次第に複雑になってきています。もともとの決定木の考え方は簡単でしたが、勾配ブースティング決定木になると複数の決定木がどのように関連しているのか、何が予測値に影響を与えているのかなどはわかりにくくなっています。

　ここで、ようやく本題である柏山さんの研究に入ってきます。柏山さんは、勾配ブースティング決定木に出てくるたくさんの決定木を可視化して、何が起きているのかを把握しやすくするという研究を行いました。柏山さんの属する伊藤研究室では、さまざまな情報可視化の研究を行っています。情報可視化というのは、複雑なものがあったときにそれを誰にでもわかりやすい形で理解できるように提示する分野です。その中でも柏山さんは勾配ブースティング決定木に出てくるたくさんの決定木の間の関係をわかりやすく提示するシステムを作成しました。

　決定木の可視化なら、最も単純なものとして図１などを思い浮かべるかも知れません。でも、柏山さんが対象としているのは決定木ひとつではなく、勾配ブースティング決定木に出てくるたくさんの（ときに何十個、何百個の）決定木の間の関係です。ひとつの決定木だけをわかりやすく表示するのではなく、図２や図３などの決定木が大量にある状態で、その間の関係をわかりやすく提示しようというのが柏山さんの研究テーマです。

　勾配ブースティング決定木を可視化するにあたって、柏山さんは (1) 大量の決定木全体の様子を把握する方法、(2) 各決定木の表現、(3) 決定木間の関係の表現の 3 点に着目しました。以下、順に説明していきます。

　(1) 大量の決定木を可視化するためには、それぞれの決定木をコンパクトに表現した上で、それら全体を把握できる形に配置しなくてはなりません。これだけの情報を画面に表示するとなると、平面的な 2 次元の表現では限界があります。そこで、柏山さんはひとつの決定木の情報を 3 次元空間の中の xy 平面におさめて、z 軸方向に大量の決定木を配置することにしました。実際の可視化結果は後で示しますが、感じとしては DNA の螺旋構造を立体図形で表現し、それを好きな方向から眺められるようなものを想像してください。このようにすることで、大量の決定木の情報をいろいろな角度から観察することができるようになります。

　(2)次に、xy 平面上に表現する各決定木の情報についてです。決定木は、質問と予測結果から構成されています。ですが、このような決定木が何百もあったとすると、各々の質問と予測値を全て提示するのは現実的ではありません。そこで、柏山さんは「質問に答えると予測値が得られる」という発想を逆転させて「各データには予測値が付随している。その予測値になる理由は質問を見るとわかる」と解釈し、xy 平面上には各データと予測値のみを表示するようにしました。例えば、図２、図３の決定木なら、それぞれ以下のようなイメージで表現します。

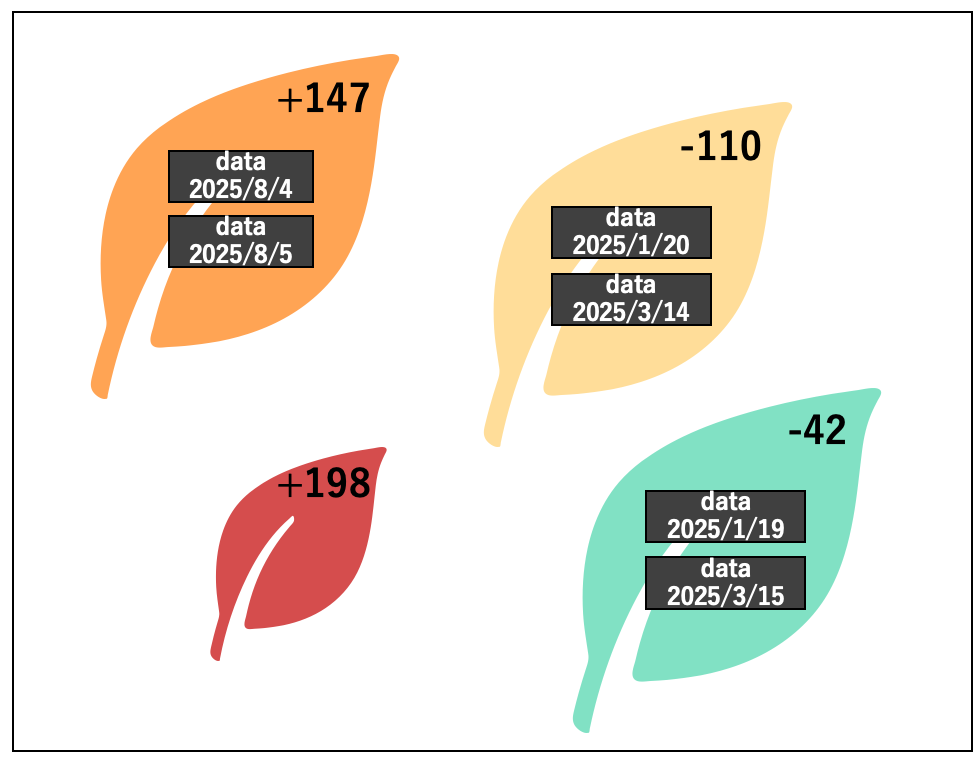
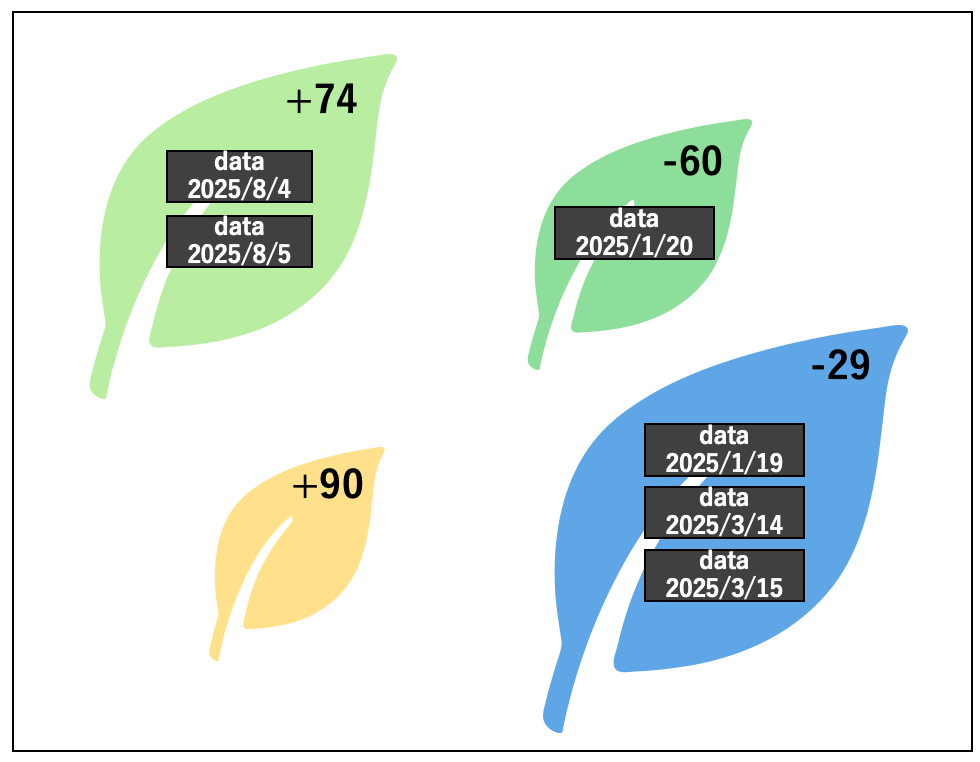
　これらの図では、ひとつの葉に同じ予測値を持つものがまとめられています。同じ予測値のものを「葉」と呼んでいるのは、これらが各決定木の一番下の予測値のところと対応しているからです。情報科学の言葉では、決定木の一番下の部分のことを「葉」と表現します。また、葉の大きさは中に入っているデータの数、色は平均予測誤差を示しています。さらに、葉の間の距離は、中のデータが似ているほど近い位置に配置されています。例えば、図５では、予測値 -29 のところに多くの日が入っているため葉が大きくなっています。また、色は予測誤差が大きいと赤、小さいと青に近くなるように設定しています。例えば、図５の予測値 -29 のところは、予測誤差の絶対値が比較的、小さいので青くなっていますが、図４の予測値 +147（や +198）のところは予測誤差の絶対値が大きくなっているので、赤に近い色がついています。このように、大きさや距離、色などを上手に使って多くの情報を表現しています。

　上に示した図では、わかりやすいように予測値と日付を書いていますが、実際に作成した可視化システムでは、大量の決定木が表示されると煩雑になってしまうため、これらは表示されません。ですが、各葉をクリックすることで予測値や各データの情報、さらにどのような質問でその予測値に至ったのかなどの情報も表示されるようになっています。こうすることで、各決定木でデータがどのように分類され、どのくらいの誤差があるのかをわかりやすく表現しています。

　(3)各決定木の情報を上のように表現すると、決定木間の関係もわかりやすく表現できるようになります。図４と図５をそれぞれ 3 次元に配置したのが以下の図です。

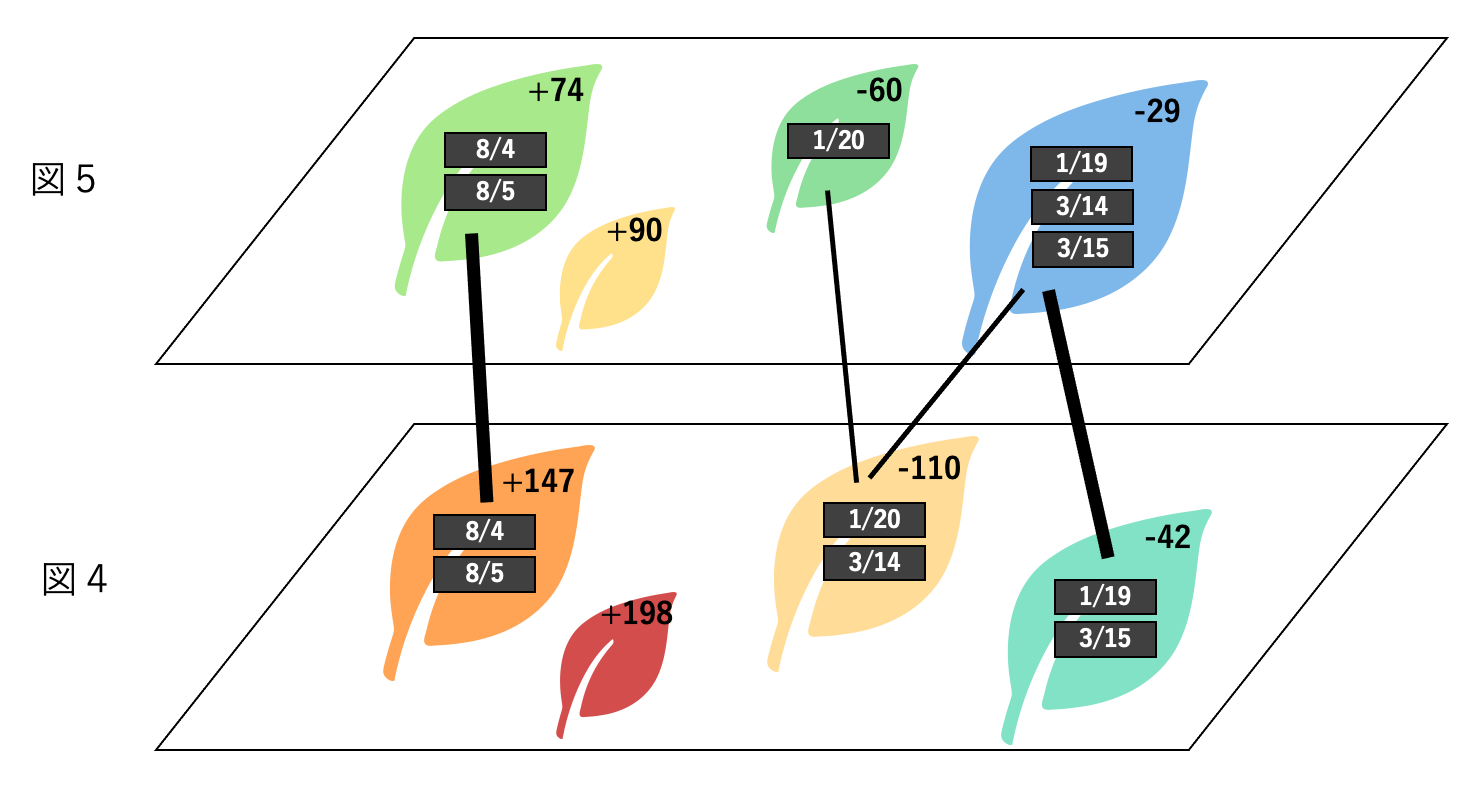
　図６では、各決定木の情報に加えて、その間の関係が線で示されています。この線は、同じ日付のデータを含む葉の間に引かれています。例えば、図６の一番左の +74 と +147 を結ぶ線は 8/4, 8/5 のデータが上下で共通しているために引かれています。また、-29 と -110 を結んでいる線は 3/14 のデータを表現しています。線の太さは、共通しているデータの個数に比例しています。このように表現すると、上下の決定木の似ている具合が線の太さで把握できるようになります。また、3/14 のデータなど、上下で異なるグループに属するデータの発見も容易になり、決定木の移り変わりが視覚的に理解できるようになります。

　このようにして作られた可視化システムの実際の運用画面が次の図７です。

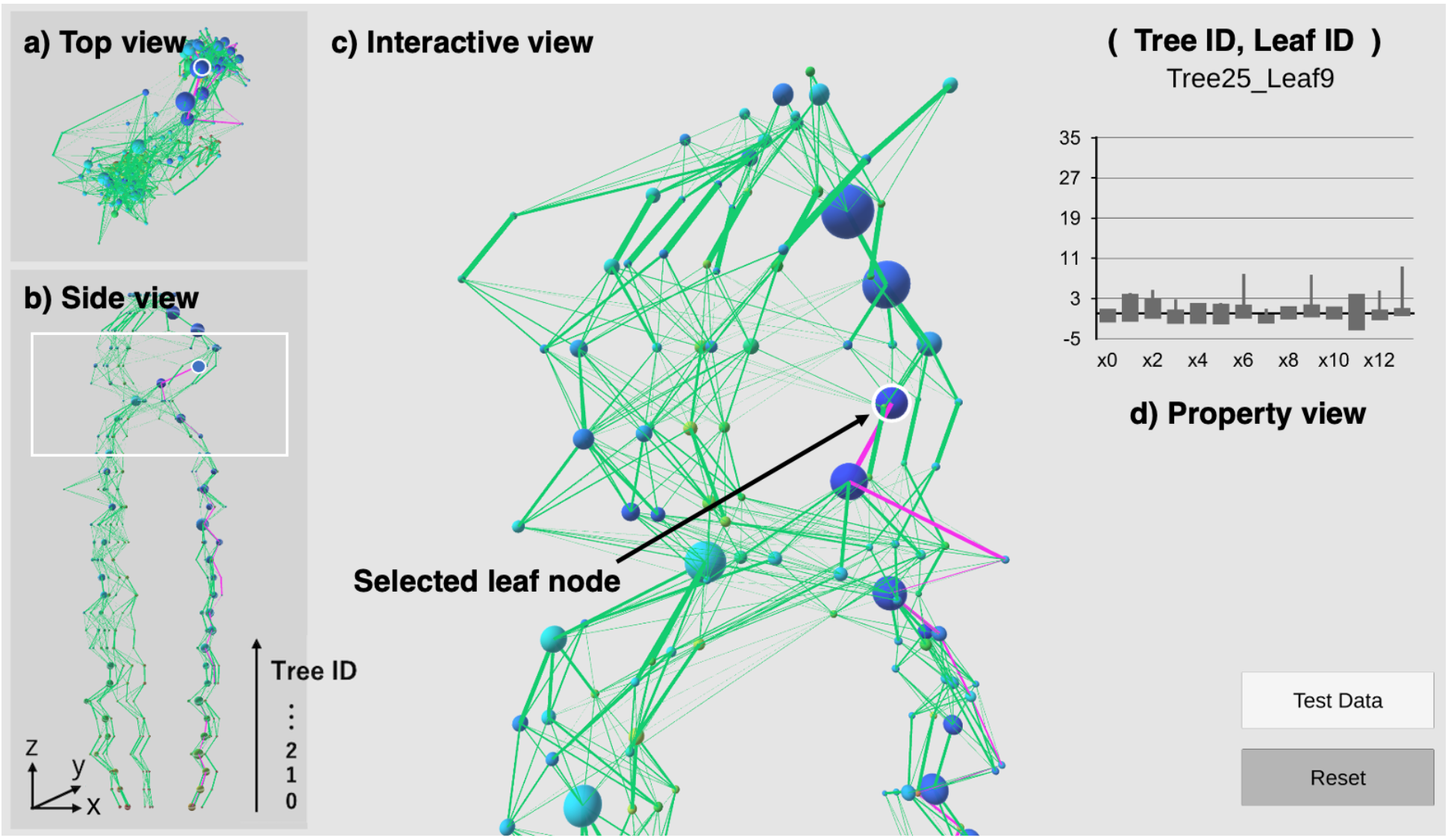
　図７の左上の図 a) が可視化した決定木を上から見たもの、b) が横から見たものです。一番下 (z=0) に最初の決定木が配置されており、順に学習していった決定木がその上に積み重なっています。真ん中の c) が一部を拡大したもので、この図は回転させたり拡大縮小したりして、詳しく好きな場所を見ることができます。また（図７では球で表現されている）葉をクリックするとそのデータの詳しい情報が d) のところに表示されるとともに、その中のデータたちが上下の決定木でどこに属していたのかも赤い線となって表示されます。このようなシステムを使って複雑な決定木を理解しようというわけです。

実データに対する可視化結果

　このシステムを実際の大きなデータに対して適用してみると、いろいろなことがわかってきます。ここでは 3 つほど例を紹介しましょう。

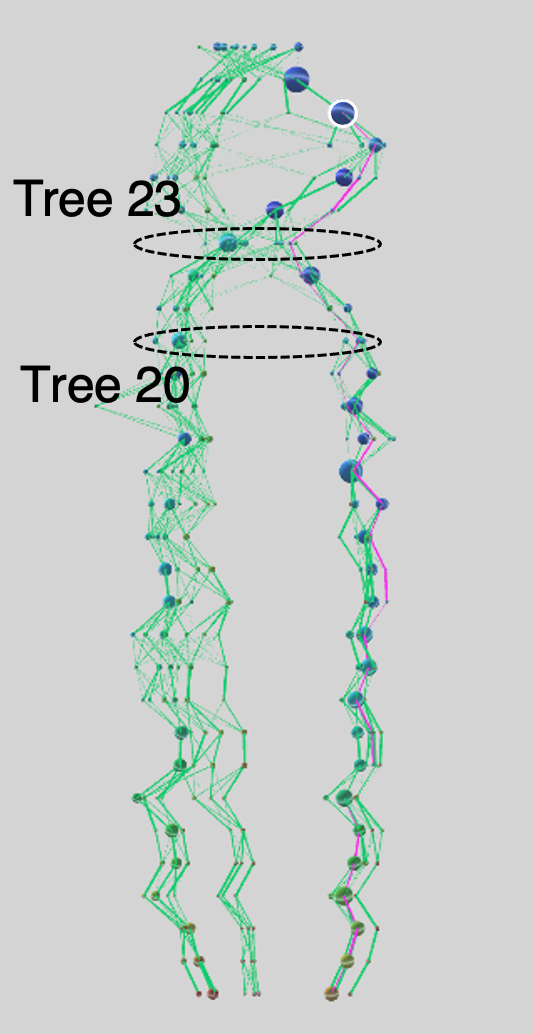
　図８ は、30 個の決定木を可視化したものです。この図を見ると、ずっと木がふたつの部分に分かれていますが、それが 23 番目の木で一度、ひとつにまとまり、その後、再びふたつの部分に分かれています。23 番目の木で一度、決定木の大きな再編が行われたけれど、結局、もとの決定木に近いもの戻っているのです。これは、そもそものデータが大きくふたつに分かれていて、それぞれ別に解析した方が精度が上がりそうなことを示唆しています。柏山さんの可視化システムを使うと、このような観察を誰でも容易に行うことができるようになります。

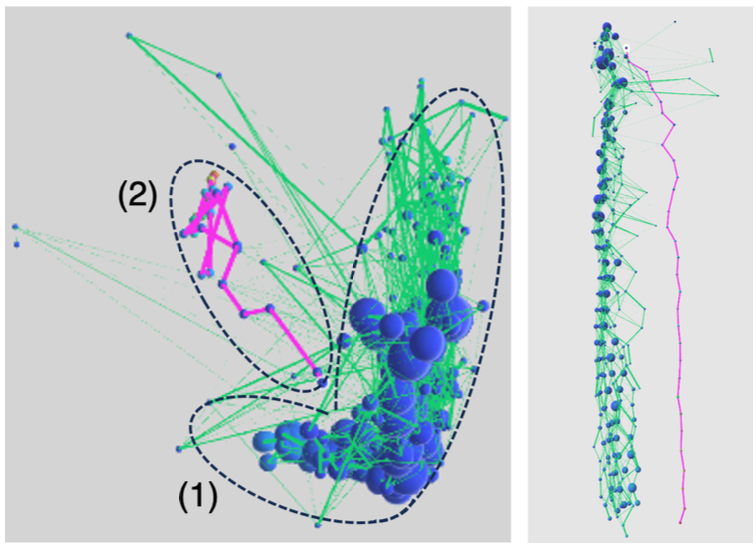
　図９は、別のデータを可視化したもので、左は上から見た図、右は側面から見た図になっています。この図でもデータがふたつに分割できそうなことがわかります。ほとんどのデータは図９左の (1) と書かれた部分に集中していますが、(2) の部分にそれとは明らかに異なるデータが存在しています。赤くなっている (2) に対応する部分は、右の図でも赤く示されています。こちらを見てもこれらのデータは他のデータとは明らかに異なる道をたどっています。実際、詳しくデータを調べて見ると、これらのデータはその特徴が大きく異なっており、外れ値になっていることがわかりました。精度の良い予測をするためには、このような外れ値を上手に分離するのは重要ですが、柏山さんの可視化システムはその検出にも大きく役立ちそうです。

　柏山さんの可視化システムは、次々と変化していくデータの特徴を調べる際にも有効です。図１０の左側の図は、あらかじめ与えられたデータに対して作成した決定木を可視化したものです。一方、右側の図は、この決定木に新たなデータを流した際の様子を可視化したものです。両者を比較すると、右側の図では多くの赤の破線が観察できます。決定木間の関係は、同じデータを含む場合に線でつなぐと説明しましたが、柏山さんの可視化システムではさらに追加機能として、これまでに観察されていなかった部分に線がつながった場合、つまりこれまでには存在していなかったタイプのデータが見つかった場合、そこの部分を赤の破線で示す機能が実装されています。図１０の右側の図に現れている赤の破線は、最初の決定木を作る際には存在しなかったデータが新たに多く出現したことを表しています。

　さらに、右側の図では球の色のつけ方を左側の図とは別にしています。左側の図では、これまでに説明した通り、予測誤差が大きければ赤に近い色、小さければ青に近い色をつけていますが、右側の図では、左側の図と比べて誤差がどう変化したかによって色をつけています。左側の図よりも誤差が大きくなったら赤、同程度であれば白、小さくなっていたら青をつけています。右側の図を見ると、球の色が赤味がかっているものが多く観察されますが、これは、新しいデータに対する予測誤差が大きくなったことを表しています。つまり、最初の決定木（左側の図）が与えられたデータの特徴を捉え過ぎていて別のデータに対しては誤差が大きくなっていた、言い方を変えると、与えられたデータの特徴を過学習していたということを示唆しています。

　ここにあげた色々な可視化の例は、そのデータ自身が何を意味しているのかを理解しなくても、いろいろな観察を行えていることに注目してください。このように柏山さんの可視化システムは誰でも気軽に使えるものになっています。

　多くのデータがあふれかえる現代、そこから色々な知見を得るデータサイエンスがますます注目を集めるようになっています。データサイエンスの分野では、データの意味するところを理解して社会に役立てようとしていますが、データの量があまりに膨大になり、適切な可視化手段がないと先に進むのが難しくなってきています。そんな中、柏山さんの構築した可視化システムは、可視化の専門家でなくても使える有用なツールになっており、今後、データサイエンスの専門家が多くのデータを扱う際の大きな助けになるものとなっています。このような可視化システムがあって初めて大量のデータを扱うことが可能になるといっても過言ではないでしょう。

バックナンバー

問い合わせ先

大学へのお問合せはこちらをご覧ください

〒112-8610　東京都文京区大塚2-1-1
TEL : 03-5978-5704
FAX : 03-5978-5705
責任者 : 情報科学科HP運営委員会　伊藤貴之


※このウェブサイトは情報科学科の学生によって制作されています。